Linear Linked Structure

1. What Are Linear Structures?

2. The Unordered Linked List

3. The Ordered Linked List

4. Other types of Linked list

3.19 Lists

Throughout the discussion of basic data structures, we will use Python lists to implement the abstract data types presented. However, other types of data structure exists.

A list is a collection of items where each item holds a relative position with respect to the others. More specifically, we will refer to this type of list as an unordered list. We can consider the list as having a first item, a second item, a third item, and so on. For simplicity we will assume that lists cannot contain duplicate items.

3.20 The Unordered Linked List

The structure of an unordered list is a collection of items where each item holds a relative position with respect to the others. Some possible unordered list operations are given below:

• List() creates a new list that is empty. It needs no parameters and returns an empty list.
• add(item) adds a new item to the head of list. It needs the item and returns nothing. Assume the item is not already in the list.
• remove(item) removes the item from the list. It needs the item and modifies the list. Raise an error if the item is not present in the list.

• search(item) searches for the item in the list. It needs the item and returns a Boolean value.
• is_empty() tests to see whether the list is empty. It needs no parameters and returns a Boolean value.
• size() returns the number of items in the list. It needs no parameters and returns an integer.

• append(item) adds a new item to the end of the list making it the last item in the collection. It needs the item and returns nothing. Assume the item is not already in the list.
• index(item) returns the position of item in the list. It needs the item and returns the index. Assume the item is in the list.

• insert(pos, item) adds a new item to the list at position pos. It needs the item and returns nothing. Assume the item is not already in the list and there are enough existing items to have position pos.
• pop() removes and returns the last item in the list. It needs nothing and returns an item. Assume the list has at least one item.
• pop(pos) removes and returns the item at position pos. It needs the position and returns the item. Assume the item is in the list.

3.21 Implementing an Unordered Linked List: Linked Lists

In order to implement an unordered list, we will construct what is commonly known as a linked list. Recall that we need to be sure that we can maintain the relative positioning of the items. However, there is no requirement that we maintain that positioning in contiguous memory.

For example, consider the collection of items. It appears that these values have been placed randomly.

If we can maintain some explicit information in each item, namely the location of the next item, then the relative position of each item can be expressed by simply following the link from one item to the next.

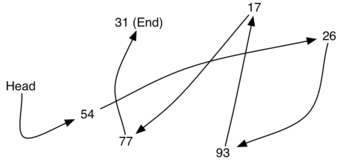
It is important to note that the location of the first item of the list must be explicitly specified. Once we know where the first item is, the first item can tell us where the second is, and so on. The external reference is often referred to as the head of the list. Similarly, the last item needs to know that there is no next item.

3.21.1 The Node Class

The basic building block for the linked list implementation is the node. Each node object must hold at least two pieces of information. First, the node must contain the list item itself. We will call this the data field of the node. In addition, each node must hold a reference to the next node.

class Node:
    """A node of a linked list"""
    def __init__(self, node_data):
        self._data = node_data
        self._next = None
    def get_data(self):
        """Get node data"""
        return self._data
    def set_data(self, node_data):
        """Set node data"""
        self._data = node_data

    def get_next(self):
        """Get next node"""
        return self._next
    def set_next(self, node_next):
        """Set next node"""
        self._next = node_next
    
    data = property(get_data, set_data)
    next = property(get_next, set_next)

Note that hidden fields _data and _next of the Node class are turned into properties and can be accessed as data and next, respectively!

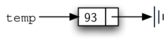
We create Node objects in the usual way.

temp = Node(93)
temp.data

93

The special Python reference value None will play an important role in the Node class and later in the linked list itself. A reference to None will denote the fact that there is no next node.

Note in the constructor that a node is initially created with next set to None. It is always a good idea to explicitly assign None to your initial next reference values.

3.21.2 The UnorderedList Class

The unordered list will be built from a collection of nodes, each linked to the next by explicit references. With this in mind, the UnorderedList class must maintain a reference to the first node. Code below shows the constructor. Note that each list object will maintain a single reference to the head of the list.

class UnorderedList:
    def __init__(self):
        self.head = None

my_list = UnorderedList()

The assignment statement creates the linked list representation

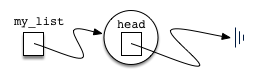
As we discussed in the Node class, the special reference None will again be used to state that the head of the list does not refer to anything. Eventually, the example list given earlier will be represented by a linked list as shown below:

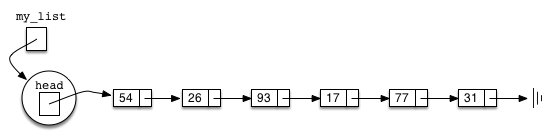
The head of the list refers to the first node which contains the first item of the list. In turn, that node holds a reference to the next node (the next item), and so on.

It is very important to note that the UnorderedList class itself does not contain any node objects. Instead it contains a single reference to only the first node in the linked structure.

The is_empty() method, shown below, simply checks to see if the head of the list is a reference to None. The result of the boolean expression self.head == None will only be true if there are no nodes in the linked list.

def is_empty(self):
    return self.head == None

So how do we get items into our list? We need to implement the add() method. However, before we can do that, we need to address the important question of where in the linked list to place the new item.

Since this list is unordered, the specific location of the new item with respect to the other items already in the list is not important. The new item can go anywhere. With that in mind, it makes sense to place the new item in the easiest location possible.

Recall that the linked list structure provides us with only one entry point, the head of the list. All of the other nodes can only be reached by accessing the first node and then following next links. This means that the easiest place to add the new node is right at the head, or beginning, of the list

my_list.add(31)
my_list.add(77)
my_list.add(17)
my_list.add(93)
my_list.add(26)
my_list.add(54)

Note that since 31 is the first item added to the list, it will eventually be the last node on the linked list as every other item is added ahead of it. Also, since 54 is the last item added, it will become the data value in the first node of the linked list.

Therefore, we can create a new node and places the item as its data. Now we must complete the process by linking the new node into the existing structure.

def add(self, item):
    temp = Node(item)
    temp.set_next(self.head)
    self.head = temp

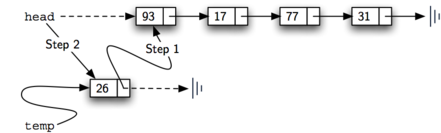
The order of the two steps described above is very important. What happens if the order of line 3 and line 4 is reversed?

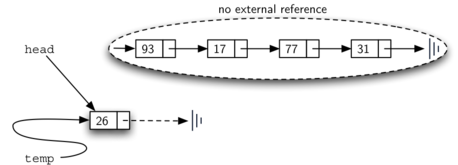
Since the head was the only external reference to the list nodes, all of the original nodes are lost and can no longer be accessed.

The next methods that we will implement – size(), search(), and remove() – are all based on a technique known as linked list traversal. Traversal refers to the process of systematically visiting each node.

To do this we use an external reference that starts at the first node in the list. As we visit each node, we move the reference to the next node by "traversing" the next reference.

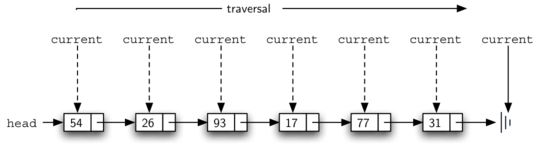
To implement the size() method, we need to traverse the linked list and keep a count of the number of nodes that occurred.

def size(self):
    current = self.head
    count = 0
    while current is not None:
        count = count + 1
        current = current.get_next()

    return count

Searching for a value in a linked list implementation of an unordered list also uses the traversal technique. As we visit each node in the linked list we will ask whether the data stored there matches the item we are looking for.

def search(self, item):
    current = self.head
    while current is not None:
        if current.data == item:
            return True
        current = current.get_next()

    return False

If we do get to the end of the list, that means that the item we are looking for must not be present. Also, if we do find the item, there is no need to continue.

my_list.search(17)

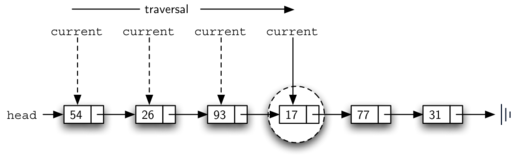
Since 17 is in the list, the traversal process needs to move only to the node containing 17. At that point, the condition in line 4 becomes True and we return the result of the search.

The remove() method requires two logical steps. First, we need to traverse the list looking for the item we want to remove. Once we find the item, we must remove it. If the item is not in the list, our method should raise a ValueError.

The first step is very similar to search. Starting with an external reference set to the head of the list, we traverse the links until we discover the item we are looking for.

When the item is found and we break out of the loop, current will be a reference to the node containing the item to be removed. But how do we remove it?

In order to remove the node containing the item, we need to modify the link in the previous node so that it refers to the node that comes after current. Unfortunately, there is no way to go backward in the linked list. Since current refers to the node ahead of the node where we would like to make the change, it is too late to make the necessary modification!

The solution to this dilemma is to use two external references as we traverse down the linked list. current will behave just as it did before, marking the current location of the traversal. The new reference, which we will call previous, will always travel one node behind current. That way, when current stops at the node to be removed, previous will refer to the proper place in the linked list for the modification!

def remove(self, item):
    current = self.head
    previous = None

    while current is not None:
        if current.data == item:
            break
        previous = current
        current = current.get_next()

    if current is None:
        raise ValueError("{} is not in the list".format(item))
    if previous is None:
        self.head = current.get_next()
    else:
        previous.next = current.get_next()

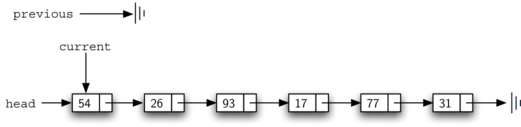
Figure below shows the movement of previous and current as they progress down the list looking for the node containing the value 17.

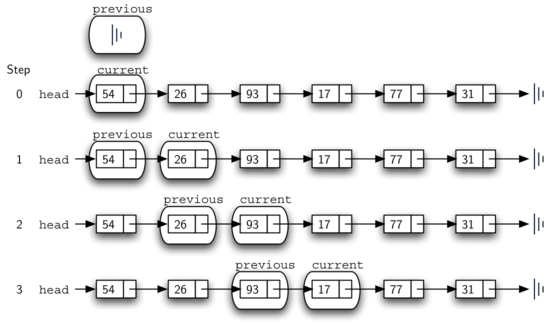
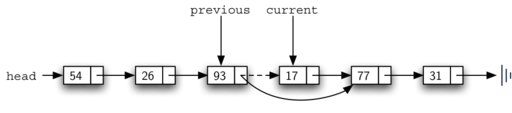
Once the searching step of the remove has been completed, we need to remove the node from the linked list. Figure above shows the link that must be modified.

However, there is a special case that needs to be addressed. If the item to be removed happens to be the first item in the list, then current will reference the first node in the linked list. This also means that previous will be None. We said earlier that previous would be referring to the node whose next reference needs to be modified in order to complete the removal. In this case, it is not previous but rather the head of the list that needs to be changed.

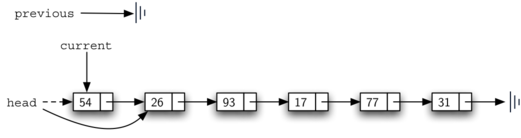
Line 13 allows us to check whether we are dealing with the special case described above. If previous did not move, it will still have the value None when the loop breaks. In that case, the head of the list is modified to refer to the node after the current node (line 14), in effect removing the first node from the linked list. However, if previous is not None, the node to be removed is somewhere down the linked list structure.

In this case the previous reference is providing us with the node whose next reference must be changed. Line 16 modifies the next property of the previous to accomplish the removal. Note that in both cases the destination of the reference change is current.get_next().

You could also add a header node to simplify the process and this is left as exercise.

import sys
sys.path.append("../pythonds3/")

from pythonds3.basic import UnorderedList

my_list = UnorderedList()

my_list.add(31)
my_list.add(77)
my_list.add(17)
my_list.add(93)
my_list.add(26)
my_list.add(54)

print(my_list)
print(my_list.size())
print(my_list.search(93))
print(my_list.search(100))

[54, 26, 93, 17, 77, 31]
6
True
False

my_list.add(100)
print(my_list.search(100))
print(my_list.size())

my_list.remove(54)
print(my_list.size())
my_list.remove(93)
print(my_list.size())
my_list.remove(31)
print(my_list.size())
print(my_list.search(93))

True
7
6
5
4
False

3.22. The Ordered Linked List

We will now consider a type of list known as an ordered list. For example, if the list of integers shown in previous section were an ordered list (ascending order), then it could be written as 17, 26, 31, 54, 77, and 93.

The structure of an ordered list is a collection of items where each item holds a relative position that is based upon some underlying characteristic of the item. The ordering is typically either ascending or descending and we assume that list items have a meaningful comparison operation that is already defined.

Many of the ordered list operations are the same as those of the unordered list:

• OrderedList() creates a new ordered list that is empty. It needs no parameters and returns an empty list.
• add(item) adds a new item to the list making sure that the order is preserved. It needs the item and returns nothing. Assume the item is not already in the list.
• remove(item) removes the item from the list. It needs the item and modifies the list. It will raise an error if the item is not present in the list.
• search(item) searches for the item in the list. It needs the item and returns a Boolean value.

• is_empty() tests to see whether the list is empty. It needs no parameters and returns a Boolean value.
• size() returns the number of items in the list. It needs no parameters and returns an integer.
• index(item) returns the position of an item in the list. It needs the item and returns the index. Assume the item is in the list.
• pop() removes and returns the last item in the list. It needs nothing and returns an item. Assume the list has at least one item.
• pop(pos) removes and returns the item at position pos. It needs the position and returns the item. Assume the item is in the list.

3.23 Implementing an Ordered Linked List

The ordered list of integers given above (17, 26, 31, 54, 77, and 93) can be represented by a linked structure as shown below.

Again, the node and link structure is ideal for representing the relative positioning of the items.

To implement the OrderedList class, we will use the same technique as seen previously with unordered lists. Once again, an empty list will be denoted by a head reference to None:

class OrderedList:
    def __init__(self):
        self.head = None

As we consider the operations for the ordered list, we should note that the is_empty() and size() methods can be implemented the same as with unordered lists since they deal only with the number of nodes in the list without regard to the actual item values.

Likewise, the remove() method will work just fine since we still need to find the item and then link around the node to remove it. The two remaining methods, search() and add(), will require some modification.

The search() of an unordered linked list required that we traverse the nodes one at a time until we either find the item we are looking for or run out of nodes (None).

t turns out that the same approach would work with the ordered list and no changes are necessary if the item is in the list. However, in the case where the item is not in the list, we can take advantage of the ordering to stop the search as soon as possible.

For example, Figure below shows the ordered linked list as a search is looking for the value 45:

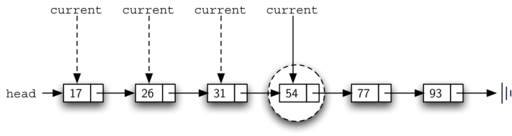
The code below shows the complete search() method. It is easy to incorporate the new condition discussed above by adding another check (line 6):

def search(self,item):
    current = self.head
    while current is not None:
        if current.data == item:
            return True
        if current.data > item:
            return False
        current = current.next

    return False

We can continue to look forward in the list (line 3). If any node is ever discovered that contains data greater than the item we are looking for, we will immediately return False.

The most significant method modification will take place in add(). Recall that for unordered lists, the add method could simply place a new node at the head of the list. It was the easiest point of access.

Unfortunately, this will no longer work with ordered lists. It is now necessary that we discover the specific place where a new item belongs in the existing ordered list.

Assume we have the ordered list consisting of 17, 26, 54, 77, and 93 and we want to add the value 31. The add method must decide that the new item belongs between 26 and 54:

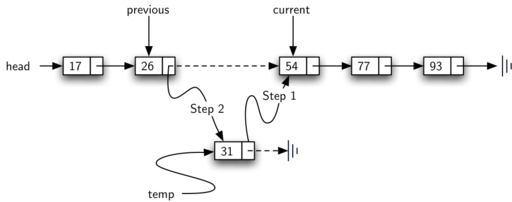
As we explained earlier, we need to traverse the linked list looking for the place where the new node will be added!

As we saw with unordered lists, it is necessary to have an additional reference, again called previous, since current will not provide access to the node that must be modified.

def add(self, item):
    """Add a new node"""
    current = self.head
    previous = None
    temp = Node(item)

    while current is not None and current.data < item:
        previous = current
        current = current.next

    if previous is None:
        temp.next = self.head
        self.head = temp
    else:
        temp.next = current
        previous.next = temp

The OrderedList class with methods discussed thus far can be found below:

from pythonds3.basic import OrderedList

my_list = OrderedList()

my_list.add(31)
my_list.add(77)
my_list.add(17)
my_list.add(93)
my_list.add(26)
my_list.add(54)

print(my_list)
print(my_list.size())
print(my_list.search(93))
print(my_list.search(100))

[17, 26, 31, 54, 77, 93]
6
True
False

3.23.1 Analysis of Linked Lists

To analyze the complexity of the linked list operations, we need to consider whether they require traversal.

Consider a linked list that has $n$ nodes. The is_empty() method is $O(1)$ since it requires one step to check the head reference for None. size(), on the other hand, will always require $n$ steps since there is no way to know how many nodes are in the linked list without traversing from head to end. Therefore, size() is $O(n)$.

Adding an item to an unordered list will always be $O(1)$ since we simply place the new node at the head of the linked list. However, search() and remove(), as well as add() for an ordered list, all require the traversal process. Although on average they may need to traverse only half of the nodes, these methods are all $O(n)$ since in the worst case each will process every node in the list.

A.1 Other types of Linked list (Optional)

Circularly linked list

In the case of linked lists, there is a more tangible notion of a circularly linked list, as we can have the tail of the list use its next reference to point back to the head of the list, as shown below. We call such a structure a circularly linked list.

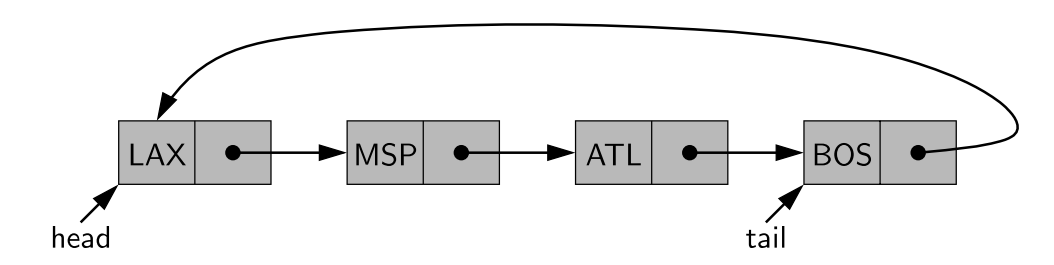
A circularly linked list provides a more general model than a standard linked list for data sets that are cyclic, that is, which do not have any particular notion of a beginning and end.

A circular view could be used, for example, to describe the order of train stops, or the order in which players take turns during a game. Even though a circularly linked list has no beginning or end, per se, we must maintain a reference to a particular node in order to make use of the list. We use the identifier current to describe such a designated node. By setting current = current.next, we can effectively advance through the nodes of the list.

Doubly linked list

In a singly linked list, each node maintains a reference to the node that is immediately after it. We have demonstrated the usefulness of such a representation when managing a sequence of elements. However, there are limitations that stem from the asymmetry of a singly linked list.

We emphasized that we can efficiently insert a node at either end of a singly linked list, and can delete a node at the head of a list, but we are unable to efficiently delete a node at the tail of the list. More generally, we cannot efficiently delete an arbitrary node from an interior position of the list if only given a reference to that node, because we cannot determine the node that immediately precedes the node to be deleted (yet, that node needs to have its next reference updated)!

To provide greater symmetry, we define a linked list in which each node keeps an explicit reference to the node before it and a reference to the node after it. Such a structure is known as a doubly linked list. These lists allow a greater variety of $O(1)$-time update operations, including insertions and deletions at arbitrary positions within the list. We continue to use the term next for the reference to the node that follows another, and we introduce the term prev for the reference to the node that precedes it.

In order to avoid some special cases when operating near the boundaries of a doubly linked list, it helps to add special nodes at both ends of the list: a header node at the beginning of the list, and a trailer node at the end of the list. These "dummy" nodes are known as sentinels (or guards), and they do not store elements of the primary sequence.

A doubly linked list with such sentinels is shown

For a nonempty list, the header’s next will refer to a node containing the first real element of a sequence, just as the trailer’s prev references the node containing the last element of a sequence.

We can treat all insertions in a unified manner, because a new node will always be placed between a pair of existing nodes. In similar fashion, every element that is to be deleted is guaranteed to be stored in a node that has neighbors on each side.

References

1. Textbook CH3